
However, from a global point of view, this projection is radically incorrect in how it shows the size of landmasses (for instance, Antarctica and Greenland seem gigantic), and furthermore, it always excludes a small region around each pole (otherwise the map would be of infinite height), so it doesn't provide a complete solution for the problem of map projection. A straight line on the map corresponds to a course of constant bearing (direction), which was very useful for nautical navigation in the past (and thus made that projection very well-known). For this reason, that projection (or a close variant) is used in several online mapping services (such as Google Maps), which means that it is frequently encountered by the general public. considering only a small part of the map, geographical features (shapes, angles) are well represented, which helps a lot in recognizing them on-the-field, or for local navigation in that small part only. It also follows that at every point the vertical and horizontal scales are the same, so locally i.e. if two roads meet at a certain angle on the surface of the Earth, they will meet at that same angle on the map. A mathematical consequence is the mapping is conformal, i.e. The main purpose of this map is to preserve compass bearings for example 13 degrees east of north will be 13 degrees clockwise from the ray pointing toward the top of the map, at every point. The Mercator projection was introduced by Flemish cartographer Gerardus Mercator in 1569.
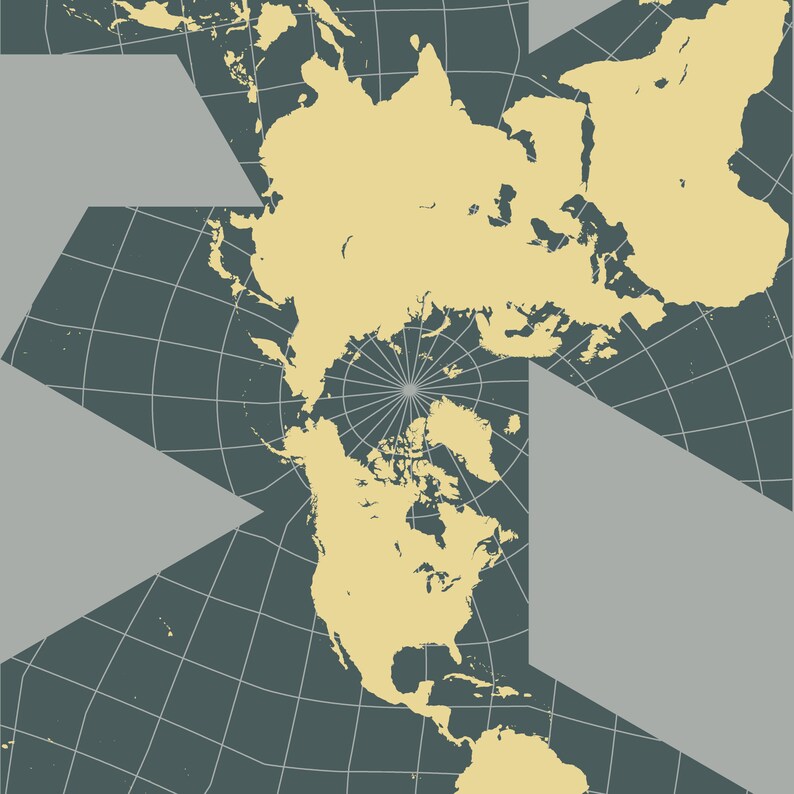
#Vectorial map world dymaxion series#
This could be inferred from the fact that he much later began publishing a series of Bad Map Projections. He may actually believe that all map projections are in a way bad. Randall suggests here the idea that someone's "favorite" map projection can reveal aspects of their personality, then goes through a series of them to show what they can mean. Some of them are more frequently used than others in mass media and therefore more well-known than others, some are purely historical and now deprecated, some are very obscure, etc. Many projections have been proposed in various contexts, each intending to minimize distortions for specific uses (for nautical navigation, for aerial navigation, for landmass size comparisons, etc.) but having drawbacks from other points of view.
There is no universal solution to this problem: Any 2D map projection will always distort in a way the spherical reality.
#Vectorial map world dymaxion how to#
Map projection, or how to represent the spherical Earth surface onto a flat support (paper, screen.) to have a usable map, is a long-time issue with very practical aspects (navigation, geographical shapes and masses visualization, etc.) as well as very scientific/mathematical ones, involving geometry or even abstract algebra among other things.


 0 kommentar(er)
0 kommentar(er)
